6.2. Incertidumbre estándar

En la Sección 6.1 se conoció que el teorema del límite central afirma que al considerar un número \(N\) de datos, determinar su media, y repetir este procedimiento muchas veces, la media de la nueva distribución de datos (medias calculadas) se apróxima a la media de la distribución original con una incertidumbre que va disminuyendo a razón de \(1/\sqrt N\). Como lo que interesa es determinar la media de la distribución original con la menor incertidumbre posible, se puede decir que el procedimiento que se acaba de describir es el adecuado. No obstante, el problema con este procedimiento es que requiere repetir la toma de los grupos de medidas varias veces, es decir, requiere que se repita el experimento varias veces. Repetir el experimento varias veces puede ser poco práctico, y en ocasiones imposible, por lo que la pregunta es ¿se puede hacer uso del teorema del límite central realizando sólo un experimento? ¿Una única toma de datos?. La repuesta es si.

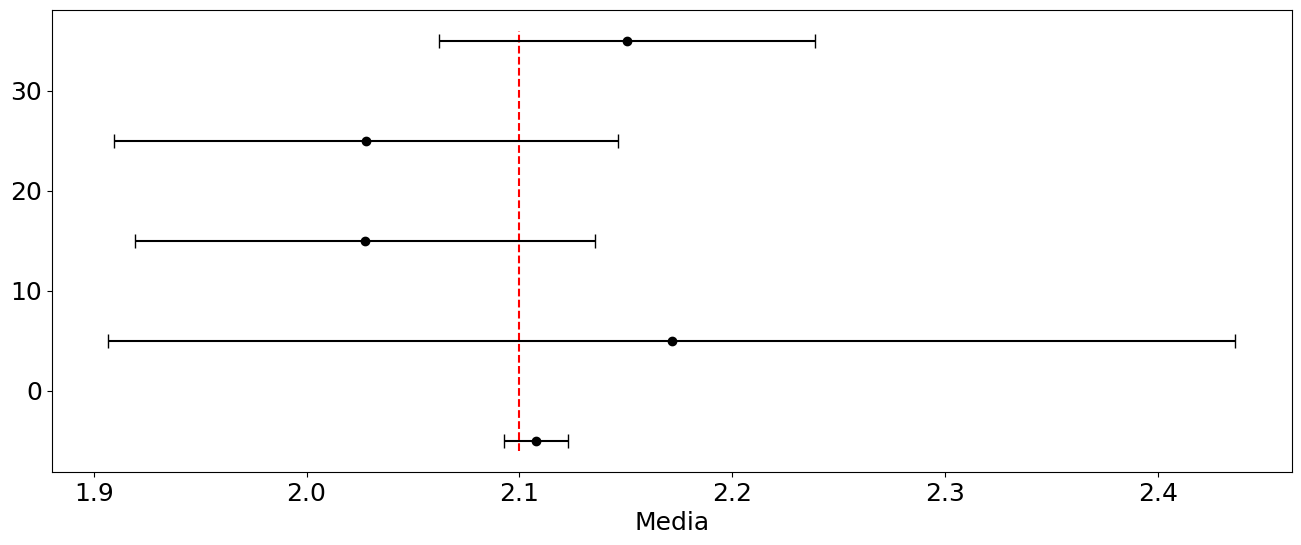
Como ejemplo de esto suponga que se tiene un experimento donde la cantidad física a medir sigue una distribución uniforme como la de la Figura 6.1, con \(\mu = 2.100\) y \(\sigma = 0.500\). Primero se mide \(35\) veces (\(N = 35\)), se determina el valor promedio, y se repite esto diez veces (\(n = 10\)) para obtener diez promedios. Con los diez promedios se obtiene la media \(\bar x = 2.108\) y la desviación estándar de la media \(s_m = \frac{s}{\sqrt{35}} = 0.015\). Ahora, una sola vez (\(n = 1\)) se mide \(N\) veces, se determina el promedio de las medidas, y se calcula la desviación estándar de la media \(s_m = \frac{s}{\sqrt N}\)[1]. En la Figura 6.2 y la Tabla 6.2 se puede observar el resultado. De la figura es claro que todos los casos predicen el valor «exacto» de la media de la distribución cuando se tiene en cuenta la incertidumbre de la medida (barras horizontales), puesto que para todos los casos la línea roja correspondiente al valor «exacto» está contenida en los rangos definidos por las barras. La única diferencia apreciable entre los casos es que algunas de las incetidumbres son menores, en particular, para el caso en que se repite \(10\) veces la toma de las \(35\) medidas, y para el caso en que se toma una sola vez \(35\) medidas, siendo mucho menor el correspondiente al primero.

Figura 6.2 Efecto del número de medidas en el experimento.

Tabla 6.2 Efecto del número de medidas en el experimento.

«Exacta»	\(\mu = 2.100\)	\(\sigma = 0.500\)
\(N = 35\), \(n = 10\)	\(\bar x = 2.108\)	\(s = 0.015\)
\(N = 5\)	\(\bar x = 2.2\)	\(s = 0.3\)
\(N = 15\)	\(\bar x = 2.03\)	\(s = 0.11\)
\(N = 25\)	\(\bar x = 2.03\)	\(s = 0.11\)
\(N = 35\)	\(\bar x = 2.15\)	\(s = 0.09\)

Se puede concluir que es valido hacer una única serie de \(N\) medidas de la variable aleatoria \(X\), y reportar el resultado del valor más probable como

(6.1)\[ X = \bar x \pm \frac{s}{\sqrt N} , \]

donde

(6.2)\[\bar x = \frac{\sum_{i=1}^{N} x_i}{N} ,\]

y

(6.3)\[ s^2 = \frac{\sum_{i=1}^{N} (x_i - \bar x)^2}{N-1} . \]

A la incertidumbre \(\frac{s}{\sqrt N}\) se le conoce como incertidumbre estándar[2].

El factor \(1/\sqrt N\) indica que a mayor número de medidas mayor precisión se tendrá en la medida. Esto se puede observar en la Figura 6.3, donde también es claro que al corresponder el factor a una función asintótica, llegará el momento donde el esfuerzo de hacer más medidas no se compensará con una mejora razonable en la precisión.

Figura 6.3 Efecto del factor \(1/\sqrt{N}\) sobre la precisión.

En la Figura 6.3 se puede apreciar que algunas veces el valor más probable obtenido se puede alejar del valor «exacto» aunque estemos aumentando el número de medidas. Igualmente, para el caso de la incertidumbre estándar, puede ocurrir que aumente aún cuando se realizan más medidas. Se debe recordar que la variable es aleatoria, y por lo tanto, puede darse el caso de que aún al medir más veces, los valores medidos se alejen más del valor «exacto», o no se distribuyan uniformemente alrededor del valor «exacto», provocando que la media obtenida se aleje del mismo o que la incertidumbre estándar aumente: es una cuestión de azar.

Advertencia

Pero tenga en cuenta que en la mayoría de los casos, de mayor interés, se desconoce cuál es el valor «exacto». Entonces, lo importante es poder confiar que el valor «exacto» siempre esté dentro de un intervalo de confianza, como veremos más adelante.

Hazlo tu mismo

Si quieres cambiar los parámetros de la Figura 6.2 para ver como pueden cambiar los resultados en virtud de la aleatoriedad, puedes usar el código que te presentamos a continuación en la ventana desplegable.

Show code cell content Hide code cell content

###################
media = 2.1    # media de la distribución original
desv = 0.5     # desviación estándar de la distribución 
semilla = 5    # semilla para el generador de valores aleatorios
N = 35         # Total de medidas por vez
n = 10         # Veces que se repite el total de medidas
##################

import numpy as np
import pylab as plt
plt.rcParams['errorbar.capsize'] = 5
plt.rcParams.update({'font.size': 18})
fig,ax = plt.subplots(1,figsize=(16,6))

def pdfUniform(media,desv):
    b = media + np.sqrt(12)*desv/2
    a = 2*media - b
    pdf = 1/(b-a)
    return a,b,pdf

#Intervalo de la distribución
a,b,pdfUni = pdfUniform(media,desv)
ax.vlines(media,-6,N+1,ls='--',color='r')
ax.set_xlabel('Media')

#Repetición del experimento n veces
np.random.seed(semilla)
newDist = []
for ii in range(n):
    newDist.append(np.mean(np.random.uniform(a,b,size=N)))

newDist_m = np.mean(newDist)
newDist_s = np.std(newDist,ddof=1)/np.sqrt(N)
ax.errorbar(newDist_m,-5,xerr=newDist_s,fmt='o',color='k')

print('Distribución original: media = {:.4f}, desv = {:.4f}'.format(media,desv))
print('Nueva distribución: {:.4f} +/- {:.4f}'.format(newDist_m,newDist_s))

#procedimiento práctico
np.random.seed(semilla)
for ii in range(5,N+1,10):
    vals = np.random.uniform(a,b,size=ii)
    Prac_m = np.mean(vals)
    Prac_s = np.std(vals,ddof=1)/np.sqrt(ii)
    print('Para {} datos: {:.4f} +/- {:.4f}'.format(ii,Prac_m,Prac_s))
    ax.errorbar(Prac_m,ii,xerr=Prac_s,fmt='o',color='k')

#ax.set_yticks(range(-5,N+1,10),['$N = 35$, $n = 10$','$N = 5$','$N = 15$', '$N = 25$', '$N = 35$'])
plt.show()

Distribución original: media = 2.1000, desv = 0.5000
Nueva distribución: 2.1078 +/- 0.0151
Para 5 datos: 2.1715 +/- 0.2648
Para 15 datos: 2.0275 +/- 0.1080
Para 25 datos: 2.0281 +/- 0.1184
Para 35 datos: 2.1505 +/- 0.0885

6.2.1. Ejemplo altura mesa: usando la incetidumbre estándar

Recordando el ejemplo de la altura de la mesa realizado en la Sección 3.5.1, los tiempos medidos por el estudiante fueron

Tabla 6.3 Tiempos de caída en centésimas de segundo.

44

53

47

47

46

50

53

Usando la ecuación (6.2), el tiempo de caída más probable es \(0.4857\,\text{s}\). Calculando la raiz cuadrada de la ecuacion (6.3), se obtiene una incertidumbre estándar de \(0.01325\,\text{s}\). Por lo tanto, el valor de tiempo de caída obtenido es: \( t = (0.486 \pm 0.013) \ \text{s} \).

Nota

La diferencia en la incetibumbre con respecto al valor obtenido con el método rápido de la Sección 3.5.1 fue de tan solo \(15\,\%\). Esta es una diferencia razonable, validando el uso del método rápido como un buen estimador de la incertidumbre, en especial para tomarlo como una primera aproximación.

Ver también

Para leer más sobre incertidumbre estándar mirar la sección 2.7 de [Hughes and Hase, 2010], secciones 4.4 y 5.6 de [Taylor, 1996], secciones 4.1 y 4.3 de [Bevington and Keith, 2001], sección 1.4.2 de [Mahecha, 2009] y secciones 3.3 y 3.4 de [Squires, 2001].

---

[1]

Por claridad, se recuerda que \(N\) corresponde al número de datos en un experimento, mientras que \(n\) se refiere al número de experimentos realizados. Por otro lado, recuerde que \(\sigma\) es la desviación estandar de la población (\(N \to \infty\)), mientras que \(s\) es la desviación estándar obtenida de una muestra, de la población, que tiene \(N\) datos.

[2]

También se le conoce como «desviación estándar de la media» o «error estándar».