2.1. Definiciones básicas#
Los conceptos a manejar para este libro son la distribución, el histograma, la media o promedio, y la desviación estándar.
2.1.1. Variable discreta y continua#
Lo primero a tener claro en un experimento al momento de hacer las medidas es el tipo de variable que se obtendrá. Considerando que todas las medidas que se hagan tienen un error inherente debido a pequeñas fluctuaciones que no se pueden controlar, y por lo tanto no permiten realizar medidas exactas[1], hablaremos de variables aleatorias. Una variable aleatoria es aquella de la cuál no se tiene ninguna certeza absoluta del valor que se obtendrá al medirla, aún habiendo realizado medidas previas. Las variables aleatorias de estudio de la estadística se pueden separar en dos tipos: discretas y continuas. Las variables discretas son aquellas que se pueden contar y cuyo valor siempre será un número entero. Ejemplos de estos pueden ser el número de autos que cruzan una calle, el número de estrellas en un área del firmamento, el número de fotones que emite una fuente en un intervalo de tiempo definido, etc. Por otro lado, las variables continuas son aquellas que no se pueden contar, y que en general se describen con un número real. Ejemplos de este tipo de variable son la temperatura en un cuarto, el diámetro de una esfera, la potencia de un láser, etc.
2.1.2. Distribución estadística#
Suponga que se hacen un total de \(N\) medidas \(x_i\). Para poder analizar la información de estas medidas lo primero que se debe hacer es organizar los datos, por ejemplo, en orden ascendente \(\{x_1, x_2, ...,x_{i-1}, x_i, x_{i+1}, ..., x_{N-1}, x_N\}\). Suponiendo que el conjunto de medidas \(x_i\) corresponde a valores enteros, se puede identificar cuales se repiten \(n\) veces tal que el valor \(x_i\) se repite \(n_i\) veces. Esta información se puede tabular de forma compacta como en la Tabla 2.1, donde \(M<N\), correspondiente al número de valores \(x_i\) diferentes.
Valor |
\(x_1\) |
\(x_2\) |
… |
\(x_i\) |
… |
\(x_{M-1}\) |
\(x_M\) |
No. repeticiones |
\(n_1\) |
\(n_2\) |
… |
\(n_i\) |
… |
\(n_{M-1}\) |
\(n_M\) |
El número total de medidas \(N\) se puede expresar como
y por lo tanto se podrá expresar el número de veces que se repite una medida en términos de una fracción
tal que \(F_i\) es la fracción de las \(N\) medidas que tienen el valor \(x_i\). El nombre de distribución estadística de las medidas se da al conjunto de las fracciones \(F_i\) que especifican cómo se distribuyen los diferentes valores de las medidas sobre todos los valores posibles.
Sumando en la ecuación (2.2) sobre los \(M\) valores diferentes y usando la ecuación (2.1), se encuentra la condición de normalización de la distribución:
2.1.3. Probabilidad#
La probabilidad es la certeza que se tiene del valor que se obtendrá en una medida. Dicho de otra forma, la probabilidad dice cuál es el chance de obtener un cierto valor al realizar una medida. A partir de la información que se obtiene de una distribución estadística, la probabilidad corresponde a la fracción \(F_i\) y puede tomar valores entre \(0\) y \(1\). También se suele expresar en términos de porcentaje:
Entonces \(P_i\) es la probabilidad en porcentaje de obtener el valor \(i\). Por ejemplo, si se dice que la probabilidad de encestar un balón de baloncesto es de \(10 \ \%\), quiere decir que de \(10\) lanzamientos hay un gran chance de encestar al menos en una ocasión. Si realizamos \(100\) lanzamientos hay un gran chance de encestar al menos en diez ocasiones. Es importante aclarar que por ser una probabilidad puede que el resultado varíe, por ejemplo para el caso de los \(100\) lanzamientos puede ocurrir que se logre encestar siete o doce veces. En definitiva, una probabilidad nunca nos dirá con absoluta certeza cuál es el resultado excepto si es del \(100 \ \%\). Si la probabilidad es del \(0 \ \%\) el resultado esperado no ocurrirá con absoluta certeza.
2.1.4. Histograma#
La representación gráfica de la distribución se conoce como histograma. Consiste en gráficar las parejas ordenadas \((x_i,F_i)\) como se muestra en Figura 2.1. También se le conoce como histograma de barras por la forma característica en la que se presentan los datos, donde la altura de la barra indica el valor de la variable.
Figura 2.1 Histograma de valores de números enteros.#
Es de notar que la suma de las alturas de todas las barras del histograma de una distribución estadística debe ser igual a uno, como lo indica la ecuación (2.3). No obstante, en ocasiones se grafica el histograma usando el número de repeticiones en reemplazo de las fracciones. Por otro lado, cuando la variable de estudio no es un entero sino un número real, se hablará de intervalos y no de barras, puesto que es imposible asignarle una barra a cada número real. Entonces, el ancho \(\Delta_i\) del intervalo[2] agrupará un rango de valores posibles de la variable de estudio, y la altura \(f_i\) del intervalo sera tal que
En la Figura 2.2 se puede observar un ejemplo de un histograma con variables de números reales, que también se le conoce como histograma de intervalos. Aunque es común que el ancho de los intervalos sea el mismo, no es una regla extricta y de hecho, en ocasiones será importante que tengan anchos diferentes. De la ecuación (2.3) queda claro que la suma de las áreas de todos los rectángulos es igual a uno.
Figura 2.2 Histograma de valores de números reales.#
2.1.5. Media o promedio#
El histograma puede dar una idea visual de como se distribuyen los datos, pero es necesario determinar otros parámetros (estadísticos) que den más información sobre la distribución de los datos. El primero de ellos es la media o promedio, que corresponde al valor alrededor del cual se distribuyen todos los demás. La definición matemática es
En la Figura 2.1 y en la Figura 2.2 se representa la posición de la media con una línea discontinua de color marrón. Dos comentarios importantes sobre la media son: frecuentemente esta coincide con el valor que más se repite en la distribución, y no necesariamente un valor de los datos de la muestra coincide con el valor de la media. Otras formas de definir la media en términos de las repeticiones y las fracciones es
2.1.6. Desviación estándar#
El otro parámetro de importancia es la desviación estándar, que indica qué tanto se dispersan los datos alrededor de la media. Una desviación estándar pequeña significa que la mayoría de los datos se distribuyen cerca de la media, mientras que una desviación estándar grande significa todo lo contrario. La definición a usar para la desviación estándar es[3]
En la Figura 2.1 y en la Figura 2.2 se representa la desviación estándar con una línea discontinua verde.
Si \(N>>1\) entonces \(N-1 \approx N\) y se podrá escribir
Esta aproximación permite escribir la siguiente expresión desarrollando el binomino de la ecaución (2.9):
es decir, el cuadrado de la desviación estándar es igual a la diferencia entre la media del cuadrado de los datos y el cuadrado de la media. Note que para la expresión (2.11) se usó una notación alternativa de promedio: \(\langle\cdot\rangle\).
2.1.7. Ejemplo uno: diámetro canicas#
Le han solicitado que verifique los diámetros de un grupo de canicas usando un vernier o calibrador. Para mostrar como se distribuyen los diámetros decide usar un histograma, y reportar el diámetro promedio y su desviación estándar.
Show code cell source
import numpy as np
import pylab as plt
import matplotlib
Ds2 = np.array([16.00,16.15,16.10,15.85,16.35,16.20,16.30,15.95,16.15,
16.35,16.35,16.10,16.30,16.25,16.20,15.50,16.50,16.15,
16.40,16.50,15.90,15.65,15.55,16.60,15.70,16.85]) # en mm, incertidumbre de 0.05 mm
media = np.mean(Ds2)
devS = np.std(Ds2,ddof=1)
matplotlib.rcParams.update({'font.size': 16})
plt.figure(figsize=(12,6))
plt.hist(Ds2, bins=[15.25,15.75,16.25,16.75,17.25], rwidth=0.98,
color='silver',density=False,cumulative=False,align='mid')
plt.vlines(media,0,11,colors='firebrick',ls='--',label=r'$\bar x$')
plt.hlines(7,media-devS,media+devS,colors='seagreen',ls='--',label=r'$\sigma$')
#plt.title('Diámetro de canicas')
plt.xlabel('Diámetro/mm')
plt.ylabel(r'Número de repeticiones')
plt.legend()
plt.grid(axis='y', alpha=0.55)
print('El diámetro promedio es {:.1f} mm con una desviación estándar de {:.1f} mm.'.format(media,devS))
El diámetro promedio es 16.2 mm con una desviación estándar de 0.3 mm.
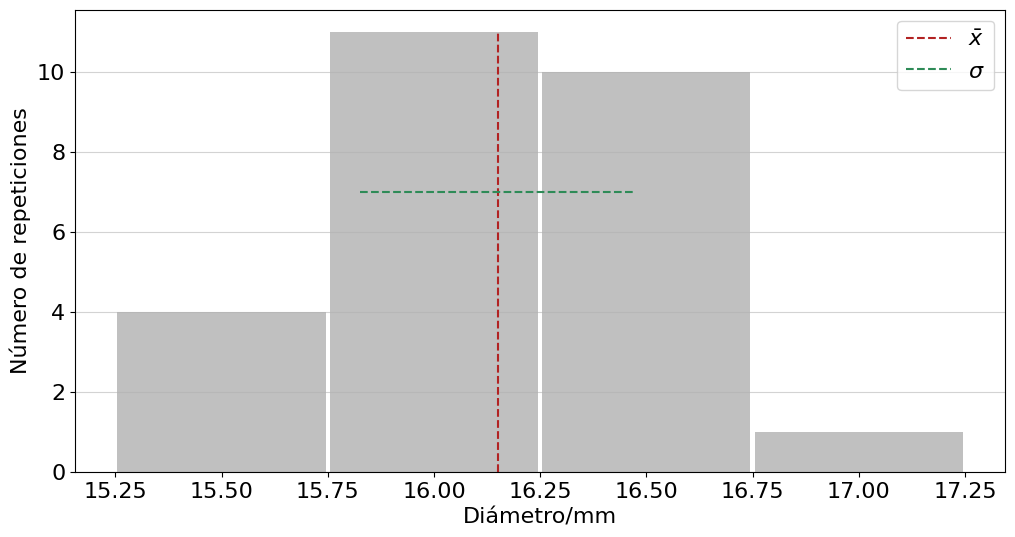
El estudio concluye que 21 de las 26 canicas tienen un diámetro entre \(15.75 \ \text{mm}\) y \(16.75 \ \text{mm}\), y solo una tiene un diámetro superior a \(16.75 \ \text{mm}\). Si usamos esta información como representativa de un grupo mayor diremos que la mayoría de las canicas tienen un diámetro entre \(15.9 \ \text{mm}\) y \(16.5 \ \text{mm}\), siendo el valor más probable \(16.2 \ \text{mm}\).
2.1.8. Ejemplo dos: altura estudiantes#
Le piden que determine como se distribuyen las alturas de los estudiantes de un curso usando una cinta métrica. Para mostrar los resultados hace uso de un histograma presentando las fracciones en porcentaje, y reporta la altura promedio y la desviación estándar en centímetros.
Show code cell source
from collections import Counter
# Altura estudiantes en cm
Ds3 = np.array([16.00,16.15,16.10,15.85,16.35,16.20,16.30,15.95,16.15,
16.35,16.35,16.10,16.30,16.25,16.20,15.50,16.50,16.15,
16.40,16.50,15.90,15.65,15.55,16.60,15.70,16.85])*10
Ds3 = np.round(Ds3) # En enteros
media = np.mean(Ds3)
devS = np.std(Ds3,ddof=1)
DS = Counter(Ds3) # Determina el número de repeticiones y almacena en lista
Dm = np.arange(155,170,1) # Alturas a graficar
### Extrae un vector de repeticiones
R = []
for ii in range(len(Dm)):
R.append(DS[Dm[ii]])
###
F = R/np.sum(R) # Fracciones
matplotlib.rcParams.update({'font.size': 16})
plt.figure(figsize=(12,6))
plt.bar(Dm,100*F,width=0.5,color='silver')
plt.vlines(media,0,25,colors='firebrick',ls='--',label=r'$\bar x$')
plt.hlines(12,media-devS,media+devS,colors='seagreen',ls='--',label=r'$2\sigma$')
#plt.title('Altura estudiantes')
plt.xlabel('Altura/cm')
plt.ylabel('Fracción/%')
plt.legend()
plt.grid(axis='y', alpha=0.55)
print('La altura promedio es {:.1f} cm con una desviación estándar de {:.1f} cm.'.format(media,devS))
La altura promedio es 161.6 cm con una desviación estándar de 3.3 cm.
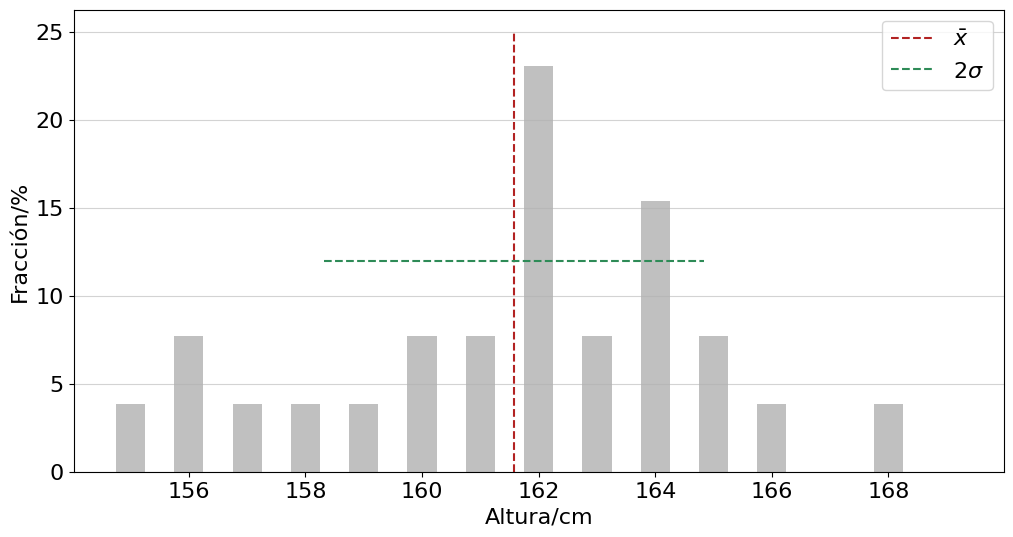
Las mediciones concluyen que la gran mayoría de los estudiantes, aproximadamente \(23 \ \%\), tienen una altura de \(162 \ \text{cm}\). Otro grupo importante de poco más del \(15 \ \%\) tienen una altura de \(164 \ \text{cm}\), mientras que el resto se distribuye de forma muy pareja entre alturas que van desde \(155 \ \text{cm}\) hasta \(168 \ \text{cm}\). Si usamos esta información como representativa de un grupo mayor diremos que la mayoría de los estudiantes tienen una altura entre \(158.3 \ \text{cm}\) y \(164.9 \ \text{cm}\), siendo el valor más probable \(161.6 \ \text{cm}\).
Ver también
Una lectura recomendada para este tema es la sección 5.1 de [Taylor, 1996].