6.6. Incertidumbre efectiva#
Según la ecuación (6.1) en principio no existe límite en el aumento de la precisión de una medida: entre más medidas \(N\) se hagan más pequeño será el factor \(1/\sqrt{N}\) y por lo tanto sólo el tiempo disponible impondrá un límite a la precisión de nuestra medida. Esta afirmación es completamente falsa, existe un límite para la máxima precisión alcanzable y es la resolución instrumental. Por lo tanto, la verdadera incertidumbre del resultado experimental se deberá determinar usando la regla de propagación de la incertidumbre para la suma, donde se considera que el valor esperado por la incertidumbre instrumental es cero. Entonces la forma más general de escribir el valor más probable de una cantidad experimental medida con su incertidumbre es:
donde \(\alpha_{inst}\) corresponde a la incertidumbre asociada al instrumento. Sin importar que tipo de distribución se le asigne a la incertidumbre asociada al instrumento (incertidumbre instrumental)[1] la versión generalizada del teorema del límite central nos asegura que la distribución que sigue la variable \(X\) es una distribución normal con media \(\bar x\) y desviación estándar \(\sqrt{ \frac{s^2}{N} + \alpha_{inst}^2 }\).
Llamaremos a la incertidumbre \(\sqrt{ \frac{s^2}{N} + \alpha_{inst}^2 }\) incertidumbre efectiva.
Advertencia
Hay que tener precaución con la anterior afirmación porque podemos no estar cumpliendo las condiciones impuestas por el teorema del límite central. No obstante, mientras las distribuciones sean simétricas y trabajemos con probabilidades cercanas a la media podemos tolerar el error que pueda surgir al considerarla una distribución normal. Más sobre el tema se puede encontrar en la página 31 del libro de Goodman [Goodman, 2000].
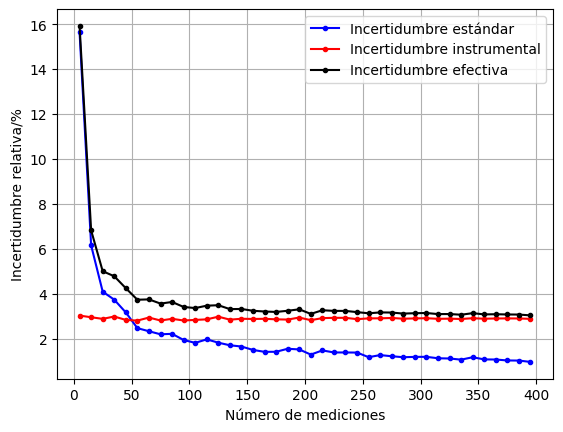
Para ilustrar mejor el concepto de la incertidumbre efectiva en la Figura 6.7 presentamos los valores de las diferentes incertidumbres a medida que se usa un mayor número de datos experimentales para determinar la incertidumbre estándar. Note como en este ejemplo para menos de 50 medidas las fluctuaciones son los suficientemente grandes para que la incertidumbre instrumental sea despreciable y por tanto sea válido medir más. En la zona alrededor de 50 medidas las incertidumbres relativas instrumental y estándar son del mismo orden por lo que es importante tener en cuenta ambas, es decir, usar la incertidumbre efectiva. Pero a medida que el número de medidas se hace significativamente mayor a 50 comienza a predominar la incertidumbre instrumental, llegando al caso extremo en que la incertidumbre estándar se hace despreciable.
Advertencia
Tenga en cuenta que aún estándo en la situación donde la incertidumbre a reportar es la instrumental porque la estándar es despreciable, el valor esperado se debe reportar usando el promedio de todas las medidas.
Figura 6.7 Comparación de incertidumbre instrumental y estándar con respecto a la incertidumbre efectiva.#
¡Hazlo tu mismo!
Para poder modificar los parámetros de la figura puedes usar el código que se presenta a continuación.
Show code cell content
import numpy as np
import pylab as plt
#### Parámetros ####
resol = 1.0 # Resolución del intrumento de medida
centro = 10. # Valor real de la cantidad física
fluct = 2.0 # Dispersión de los valores medidos debido a fluctuaciones (desviación estándar)
####################
# Determinación de la incertidumbre del instrumento suponiendo una distribución uniforme
e_resol = resol/np.sqrt(12)
# Simulación de la media y desviación estándar de la muestra para diferentes tamaños muestrales
rng = np.random.default_rng(3)
Sm = []
Xm = []
rango = np.arange(5,400,10)
for ii in rango:
xi = centro + fluct*rng.standard_normal(size=ii)
Sm.append(np.std(xi,ddof=1))
Xm.append(np.mean(xi))
# conversión de los datos a arreglos, incertidumbre estándar e incertidumbre efectiva
xm = np.asarray(Xm)
sm = np.asarray(Sm)/np.sqrt(rango)
error = np.sqrt(sm**2 + e_resol**2)
E_resol = np.ones(len(rango))*e_resol
# Gráfica de los resultados
fig, ax = plt.subplots(1)
ax.plot(rango,sm*100/xm,'b.-',label='Incertidumbre estándar')
ax.plot(rango,E_resol*100/xm,'r.-',label='Incertidumbre instrumental')
ax.plot(rango,error*100/xm,'k.-',label='Incertidumbre efectiva')
ax.set_xlabel('Número de mediciones')
ax.set_ylabel('Incertidumbre relativa/%')
plt.grid()
plt.legend()
#plt.savefig('imagenes/ResolVsFluctua.svg')
plt.show()