3.3. Precision y Exactitud#
Cuándo se realiza una medida experimental de una cantidad física, el objetivo principal es obtener el valor exacto. Desafortunadamente, en principio, nunca se podrá obtener dicho valor exacto por dos razones básicas: la primera razón se debe a las limitantes que se tienen con la instrumentación utilizada, ya sea por un error en el uso del instrumento o por una limitante propia del instrumento. La segunda razón es el hecho de que el propio fenómeno físico corresponde a un proceso aleatorio, con una incertidumbre intrínseca en el valor de la cantidad física de interés, que no tiene que ver con el proceso particular de medición.
3.3.1. Precisión#
Si al hacer medidas repetitivas de una misma cantidad física los valores encontrados son diferentes, pero están agrupados alrededor de un valor promedio, se dirá que la medida es más o menos precisa dependiendo de qué tan agrupados o no estén los valores encontrados. Cómo se verá más adelante, la precisión estará directamente relacionada con la incertidumbre aleatoria y con la reproducibilidad del resultado que se obtuvo. Se puede aumentar la precisión de una medida haciendo más medidas repetitivas o usando un instrumento más preciso, es decir, de mayor resolución. Cómo se observa en la Figura 3.1, tanto en (a) y (b) los datos son más precisos que en (c) y (d) porque están más agrupados.

Figura 3.1 Comparación entre datos precisos y exactos en la medición de la aceleración de la gravedad. La línea negra discontinua es el valor aceptado, mientras que las líneas rojas son los valores medidos. En (a) los datos tiene gran precisión y son bastante exactos, mientras que en (b) tienen la misma precisión pero son inexactos. En (c) los datos no son muy precisos pero por lo menos no son inexactos al contener al valor real. En cambio, los datos en (d) no son precisos y además son inexactos.#
3.3.2. Exactitud#
La exactitud está relacionada con el hecho de que, si bien los datos pueden tener cierta dispersión, el valor real o aceptado estará contenido dentro del rango de dispersión de los valores, y cerca del valor promedio. En caso contrario el resultado es inexacto. Cómo se verá más adelante, la exactitud está directamente relacionada con las incertidumbres sistemáticas que puedan tener los valores. Es importante aclarar tres asuntos en este momento: si se habla de valor aceptado hay seguridad de la exactitud del resultado con referencia al valor aceptado. Si se habla de valor real, este siempre será desconocido y solo es posible hablar de exactitud en caso de encontrar y eliminar algún error sistemático. Finalmente, si los datos están muy dispersos (poca precisión), aún si el valor real o aceptado está dentro del rango de datos, no tiene ningún sentido hablar de exactitud. En la Figura 3.1 se puede notar que los datos en (b) y (d) no se agrupan en torno al valor esperado por lo quen son inexactos, mientras que los datos en (a) y (c) al agruparse en torno al valor esperado se pueden considerar más exactos.
3.3.3. Ejemplo interactivo: caida libre#
El siguiente ejemplo simula unos datos experimentales del tiempo de caída libre de un objeto cuando es lanzado desde una altura \(h\) de \(2\) metros. Tomando como valor aceptado para la aceleración de la gravedad \(g = 9.77 \ \text{m s}^{-2}\) y usando la fórmula \(t = \sqrt{h/g}\), el valor aceptado de tiempo de caída será \(0.6398 \ \text{s}\). Suponiendo que las medidas con un cronómetro tendrán una dispersión debida a los errores aleatorios, controlada con el parámetro sigma, y un error en el valor inicial de tiempo debido a un error sistemático, dado por el parámetro dt. Siendo N el número de lanzamientos hechos modifique estos valores y corrobore los conceptos de precisión y exactitud.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
def legend_without_duplicate_labels(ax):
handles, labels = ax.get_legend_handles_labels()
unique = [(h, l) for i, (h, l) in enumerate(zip(handles, labels)) if l not in labels[:i]]
ax.legend(*zip(*unique))
def graf1(data):
central = np.mean(data)
eje = np.zeros(len(data))
fig , ax1 = plt.subplots(figsize=(8,3))
ax1.plot(data,eje,'r|',ms= 10,label='Datos')
ax1.vlines(0.6398,-0.15,0.3,'k',linestyle='--',label='Valor aceptado')
ax1.vlines(central,-0.1,0.2,'b',linestyle='-.',label='Valor central')
ax1.set(yticklabels=[]) # remove the tick labels
ax1.tick_params(left=False) # remove the ticks
ax1.set_xlabel('tiempo/s',fontsize=18)
ax1.set_xlim(0.1,1.1)
ax1.set_ylim(-1,1)
legend_without_duplicate_labels(ax1)
# use set_position
ax1.spines['top'].set_color('none')
ax1.spines['left'].set_color('none')
ax1.spines['right'].set_color('none')
ax1.spines['bottom'].set_position('zero')
Advertencia
Active el Live Code en la parte de arriba de la página.
La primera vez debe presionar el botón restart & run all. Posteriormente puede teclear Shift+Enter o presionar el botón run.
# Modifique los valores N, sigma y dt, y corra el programa
################
N = 9
sigma = 0.1
dt = 0.05
################
data = sigma*np.random.randn(1,N) + 0.6398 + dt
graf1(data)
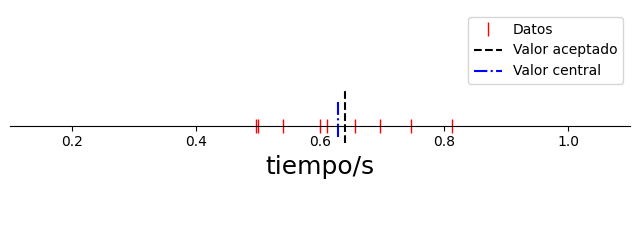
Pregunta: si su experimento tiene un error sistemático, ¿cuál es el problema de mejorar la precisión indefinidamente?
El problema está en que los errores aleatorios serán inferiores al error sistemático y por lo tanto el resultado pasará de ser exacto a ser inexacto.
Ver también
Más sobre los temas de precisión y exactitud se puede encontrar en la sección 1.2.1 de [Hughes and Hase, 2010], en la sección 4.1 y pág. 18 de [Taylor, 1996], y en la sección 1.1 de [Bevington and Keith, 2001].